Quick Start Guide

Import sire using

>>> import sire as sr

Load a molecule from a URL, via sire.load().

>>> mols = sr.load(f"{sr.tutorial_url}/p38.pdb")

Note

sire.tutorial_url expands to the base URL that contains all tutorial files.

View molecules using view().

>>> mols.view()
View of the P38 protein

Or load molecules that need multiple input files by passing in multiple files.

>>> mols = sr.load(f"{sr.tutorial_url}/ala.top", f"{sr.tutorial_url}/ala.traj")

Note

You could use sire.expand() to put sire.tutorial_url in front of ala.top and ala.crd, e.g. via sr.expand(sr.tutorial_url, ["ala.top", "ala.traj"])

There are lots of ways to search or index for molecules, e.g.

>>> mols[0]
Molecule( ACE:7   num_atoms=22 num_residues=3 )

has returned the first molecule in the system of molecules that were loaded.

>>> mols["water"]
SelectorMol( size=630
0: Molecule( WAT:4   num_atoms=3 num_residues=1 )
1: Molecule( WAT:5   num_atoms=3 num_residues=1 )
2: Molecule( WAT:6   num_atoms=3 num_residues=1 )
3: Molecule( WAT:7   num_atoms=3 num_residues=1 )
4: Molecule( WAT:8   num_atoms=3 num_residues=1 )
...
625: Molecule( WAT:629 num_atoms=3 num_residues=1 )
626: Molecule( WAT:630 num_atoms=3 num_residues=1 )
627: Molecule( WAT:631 num_atoms=3 num_residues=1 )
628: Molecule( WAT:632 num_atoms=3 num_residues=1 )
629: Molecule( WAT:633 num_atoms=3 num_residues=1 )
)

has returned all of the water molecules,

while

>>> mols[0]["element C"]
Selector<SireMol::Atom>( size=6
0:  Atom( CH3:2   [  18.98,    3.45,   13.39] )
1:  Atom( C:5     [  18.48,    4.55,   14.35] )
2:  Atom( CA:9    [  16.54,    5.03,   15.81] )
3:  Atom( CB:11   [  16.05,    6.39,   15.26] )
4:  Atom( C:15    [  15.37,    4.19,   16.43] )
5:  Atom( CH3:19  [  13.83,    3.94,   18.35] )
)

has returned all of the carbon atoms in the first molecule.

Smarts searchs are supported too! For example, here are three matches for a smarts string that finds aliphatic carbons.

>>> mols["smarts [#6]!:[#6]"]
AtomMatch( size=3
0: [2] CH3:2,C:5
1: [2] CA:9,CB:11
2: [2] CA:9,C:15
)

You can also search for bonds, e.g.

>>> mols[0].bonds()
SelectorBond( size=21
0: Bond( HH31:1 => CH3:2 )
1: Bond( CH3:2 => HH32:3 )
2: Bond( CH3:2 => HH33:4 )
3: Bond( CH3:2 => C:5 )
4: Bond( C:5 => O:6 )
...
16: Bond( N:17 => H:18 )
17: Bond( N:17 => CH3:19 )
18: Bond( CH3:19 => HH31:20 )
19: Bond( CH3:19 => HH32:21 )
20: Bond( CH3:19 => HH33:22 )
)

has returned all of the bonds in the first molecule, while

>>> mols.bonds("element O", "element H")
SelectorMBond( size=1260
0: MolNum(4) Bond( O:23 => H1:24 )
1: MolNum(4) Bond( O:23 => H2:25 )
2: MolNum(5) Bond( O:26 => H1:27 )
3: MolNum(5) Bond( O:26 => H2:28 )
4: MolNum(6) Bond( O:29 => H1:30 )
...
1255: MolNum(631) Bond( O:1904 => H2:1906 )
1256: MolNum(632) Bond( O:1907 => H1:1908 )
1257: MolNum(632) Bond( O:1907 => H2:1909 )
1258: MolNum(633) Bond( O:1910 => H1:1911 )
1259: MolNum(633) Bond( O:1910 => H2:1912 )
)

has returned all of the oxygen-hydrogen bonds in all molecules.

If a trajectory has been loaded (as is the case here) then you can get the number of frames using

>>> mols.num_frames()
500

and can view the movie using

>>> mols.view()
View of the aladip movie

The view() function can be called on any selection, so you can view the movie of the first molecule using

>>> mols[0].view()
View of first molecule in the aladip movie

You can extract a subset of trajectory frames by indexing, e.g.

>>> mols[0].trajectory()[0::100].view()
View of first molecule the subset of the aladip movie

views every 100 frames of the trajectory.

If the molecule was loaded with forcefield parameters, then you can calculate its energy using the energy() function.

>>> mols[0].energy()
31.5691 kcal mol-1

You can get all of the components via

>>> mols[0].energy().components()
{'bond': 4.22497 kcal mol-1,
 '1-4_LJ': 3.50984 kcal mol-1,
 'angle': 7.57006 kcal mol-1,
 'dihedral': 9.80034 kcal mol-1,
 '1-4_coulomb': 44.8105 kcal mol-1,
 'intra_LJ': -1.31125 kcal mol-1,
 'improper': 0.485545 kcal mol-1,
 'intra_coulomb': -37.5208 kcal mol-1}

You can calculate the energy across a trajectory, with the results returned as a pandas dataframe!

>>> mols[0].trajectory().energy()
     frame        time    1-4_LJ  1-4_coulomb      angle      bond   dihedral  improper  intra_LJ  intra_coulomb      total
0        0    0.200000  3.509838    44.810452   7.570059  4.224970   9.800343  0.485545 -1.311255     -37.520806  31.569147
1        1    0.400000  2.700506    47.698455  12.470519  2.785874  11.776295  1.131481 -1.617496     -40.126219  36.819417
2        2    0.600000  2.801076    43.486411  11.607753  2.023439  11.614774  0.124729 -1.103966     -36.633297  33.920920
3        3    0.800000  3.365638    47.483966   6.524609  0.663454  11.383852  0.339333 -0.983872     -40.197920  28.579061
4        4    1.000000  3.534830    48.596027   6.517530  2.190370  10.214994  0.255331 -1.699613     -40.355054  29.254415
..     ...         ...       ...          ...        ...       ...        ...       ...       ...            ...        ...
495    495   99.199997  2.665994    42.866319  11.339087  4.172684   9.875872  0.356887 -1.584092     -36.499764  33.192988
496    496   99.400002  3.062467    44.852774   9.268408  1.878366  10.548897  0.327064 -1.814718     -36.671683  31.451575
497    497   99.599998  3.530233    44.908117  10.487378  4.454670  10.223964  1.006034 -0.692972     -37.118048  36.799376
498    498   99.800003  3.511116    42.976288   9.017446  0.809064  10.841436  0.518190 -1.862433     -35.481467  30.329641
499    499  100.000000  3.768998    41.625135  13.629923  1.089916  11.889372  0.846805 -1.897328     -36.547672  34.405149

You can do more with the molecule, for example viewing it’s 2D structure

>>> mols[0].view2d()
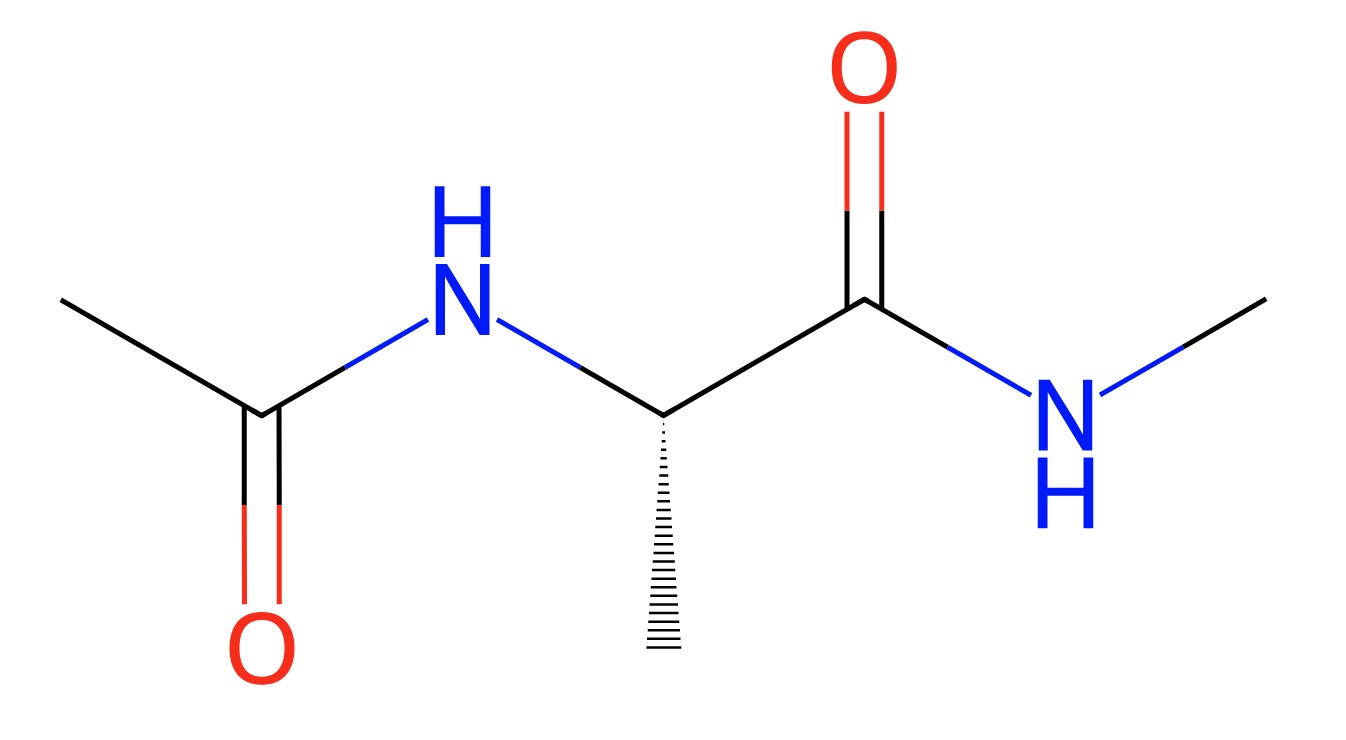
2D view of first molecule the subset of the aladip movie

or generating its smiles string.

>>> mols[0].smiles()
'CNC(=O)C(C)NC(C)=O'

You can also convert it to an RDKit molecule!

>>> rdmol = sr.convert.to(mols[0], "rdkit")

And you can even run molecular dynamics using the integration with OpenMM.

>>> mols = sr.load(sr.expand(sr.tutorial_url, "kigaki.gro", "kigaki.top"),
...                silent=True)
>>> mols.view()
3D view of the kigaki system 
>>> mols = mols.minimisation().run().commit()
>>> d = mols.dynamics(timestep="4fs")
>>> d.run("20ps", save_frequency="1ps")
>>> mols = d.commit()
>>> mols.trajectory().energy()
    frame  time     1-4_LJ  1-4_coulomb           LJ      angle          bond       coulomb    dihedral   intra_LJ  intra_coulomb         total
0       0   1.0  59.828605  1356.012783  9717.588398  34.081250  9.935577e-08 -58901.908280  145.262639 -60.009867    -830.297820 -48479.442291
1       1   2.0  59.859426  1358.426949  9721.478025  33.488730  1.020368e-07 -58977.547695  143.620760 -63.368620    -832.992328 -48557.034752
2       2   3.0  60.891111  1363.801767  9854.057685  32.568284  9.815839e-08 -59169.733258  145.274884 -62.029406    -838.669248 -48613.838181
3       3   4.0  59.832609  1357.912373  9851.460866  32.471396  2.825340e-07 -59192.703528  140.362271 -65.433697    -829.466133 -48645.563842
4       4   5.0  60.074686  1359.927851  9879.077092  34.170306  1.003672e-07 -59240.068442  139.836463 -64.083724    -833.119507 -48664.185275
5       5   6.0  59.375049  1358.601877  9886.713393  34.034265  9.092219e-08 -59270.897562  140.563988 -63.993368    -831.838422 -48687.440781
6       6   7.0  59.614215  1357.914063  9857.271105  34.639254  1.061152e-07 -59250.463890  140.829589 -64.766169    -829.218503 -48694.180337
7       7   8.0  59.926889  1361.405155  9957.054478  34.806703  3.159753e-07 -59380.997407  143.988778 -66.272231    -836.888535 -48726.976172
8       8   9.0  58.966007  1358.311827  9967.327772  34.997531  3.027917e-07 -59405.583408  142.485999 -64.733607    -831.207715 -48739.435594
9       9  10.0  60.324323  1360.640600  9939.400939  36.198475  1.166730e-07 -59388.226935  143.212016 -64.316508    -837.483867 -48750.250956
10     10  11.0  61.320326  1362.023485  9955.071224  34.056823  1.139431e-07 -59424.212266  143.513301 -64.975309    -837.997195 -48771.199611
11     11  12.0  60.415993  1362.776379  9936.669535  31.304641  9.647357e-08 -59410.580161  145.678519 -64.433834    -835.417971 -48773.586899
12     12  13.0  60.970833  1366.508370  9986.881634  33.251273  2.509407e-07 -59466.056471  144.351857 -65.429617    -841.930932 -48781.453053
13     13  14.0  60.245588  1361.266409  9986.122124  34.192312  1.163054e-07 -59480.201397  145.712628 -61.013711    -838.646145 -48792.322190
14     14  15.0  61.878785  1370.377196  9924.323617  31.399821  2.785520e-07 -59418.248563  144.305975 -64.940040    -845.430135 -48796.333344
15     15  16.0  60.430617  1365.739457  9926.082150  33.156124  2.836895e-07 -59423.448702  144.681590 -64.043674    -840.110188 -48797.512625
16     16  17.0  60.294772  1360.174160  9950.578785  32.453372  1.011507e-07 -59450.019119  143.409696 -64.041887    -835.388935 -48802.539157
17     17  18.0  61.156756  1363.542712  9947.586104  34.036896  9.579309e-08 -59452.548714  146.142252 -64.800847    -839.303707 -48804.188547
18     18  19.0  60.048626  1364.033346  9976.885470  33.771207  9.353054e-08 -59483.125256  144.011481 -64.081234    -838.157968 -48806.614328
19     19  20.0  61.609644  1363.227511  9935.113811  32.689491  2.968531e-07 -59452.910379  144.467384 -64.420695    -835.410744 -48815.633975

This integration extends to running GPU-accelerated alchemical molecular dynamics free energy calculations. For example, load up this merged molecule that uses a λ-coordinate to morph between ethane and methanol.

>>> mols = sr.load(sr.expand(sr.tutorial_url, "merged_molecule.s3"))

We’ll now select the reference state (ethane)…

>>> mols = sr.morph.link_to_reference(mols)

To calculate a free energy, we would need to run multiple simulations across λ, calculating the difference in energy between neighbouring λ-windows. How to do this is described in full here. For this quick start guide, we’ll just run at λ=0.5, calculating the difference in energy between λ=0.5 and λ=0.0 and λ=1.0.

First, lets minimise at λ=0.5.

>>> mols = mols.minimisation(lambda_value=0.5).run().commit()

And not lets run a short dynamics simulation at λ=0.5, calculating the energy differences to λ=0.0 and λ=1.0.

>>> d = mols.dynamics(lambda_value=0.5, timestep="1fs", temperature="25oC")
>>> d.run("5ps", energy_frequency="0.5ps", lambda_windows=[0.0, 1.0])

We can now extract the energy differences in an alchemlyb-compatible pandas DataFrame.

>>> print(d.commit().energy_trajectory().to_alchemlyb())
                          0.0           0.5           1.0
time fep-lambda
0.5  0.5        -46062.581449 -46066.727158 -46064.969441
1.0  0.5        -43335.286994 -43351.114108 -43348.340617
1.5  0.5        -41676.617061 -41685.901393 -41684.741190
2.0  0.5        -40392.020981 -40449.196087 -40448.185263
2.5  0.5        -39720.265484 -39743.531651 -39740.788035
3.0  0.5        -39067.899327 -39094.033563 -39092.723982
3.5  0.5        -38659.468399 -38677.805074 -38676.375989
4.0  0.5        -38354.706210 -38366.022091 -38363.577232
4.5  0.5        -38160.932310 -38175.773525 -38172.820779
5.0  0.5        -37844.757596 -37850.187961 -37848.280865

See the tutorial for a complete script to run and analyse relative free energy calculations.

This is just the beginning of what sire can do! To learn more, please take a look at the detailed guides or the tutorial.