Annihilation and Decoupling¶
So far, we have discussed how to construct merge molecules that represent perturbations from one molecule to another. These are useful for relative free energy calculations.
Absolute free energy calculations require perturbations that decouple
or annihilate molecules. The sire.morph.decouple() and
sire.morph.annihilate() create merged molecules that represent
these perturbations.
Decoupling¶
Decoupling is the process of turning off the interactions between the molecule of interest, and all other molecules in the system.
For example, let’s load up a system comprising benzene in a box of water (with some ions).
>>> import sire as sr
>>> mols = sr.load_test_files("benzene.prm7", "benzene.rst")
>>> benzene = mols[0]
>>> print(benzene)
Molecule( BEN:2 num_atoms=12 num_residues=1 )
We can create a merged molecule that represents the decoupling of the
benzene via the sire.morph.decouple() function.
>>> benzene = sr.morph.decouple(benzene, as_new_molecule=False)
>>> print(benzene)
Molecule( BEN:2 num_atoms=12 num_residues=1 )
Note
We pass in as_new_molecule=False so that the resulting merged
molecule keeps the same molecule number as the original benzene.
If we had passed in as_new_molecule=True (which is the default)
then the returned molecule would be a “new” molecule, with its
own, unique molecule number.
The decoupled benzene molecule is a merged molecule where all of the atoms are converted to ghost atoms.
>>> p = benzene.perturbation().to_openmm()
>>> print(p.changed_atoms())
atom charge0 charge1 sigma0 sigma1 epsilon0 epsilon1 alpha0 alpha1 kappa0 kappa1
0 C:1 -0.13 0.0 0.348065 0.348065 0.363503 0.0 0.0 1.0 1.0 1.0
1 C2:2 -0.13 0.0 0.348065 0.348065 0.363503 0.0 0.0 1.0 1.0 1.0
2 C3:3 -0.13 0.0 0.348065 0.348065 0.363503 0.0 0.0 1.0 1.0 1.0
3 C4:4 -0.13 0.0 0.348065 0.348065 0.363503 0.0 0.0 1.0 1.0 1.0
4 C5:5 -0.13 0.0 0.348065 0.348065 0.363503 0.0 0.0 1.0 1.0 1.0
5 C6:6 -0.13 0.0 0.348065 0.348065 0.363503 0.0 0.0 1.0 1.0 1.0
6 H1:7 0.13 0.0 0.257258 0.257258 0.065318 0.0 0.0 1.0 1.0 1.0
7 H2:8 0.13 0.0 0.257258 0.257258 0.065318 0.0 0.0 1.0 1.0 1.0
8 H3:9 0.13 0.0 0.257258 0.257258 0.065318 0.0 0.0 1.0 1.0 1.0
9 H4:10 0.13 0.0 0.257258 0.257258 0.065318 0.0 0.0 1.0 1.0 1.0
10 H5:11 0.13 0.0 0.257258 0.257258 0.065318 0.0 0.0 1.0 1.0 1.0
11 H6:12 0.13 0.0 0.257258 0.257258 0.065318 0.0 0.0 1.0 1.0 1.0
Note
Note how the atoms are converted to ghosts by setting the charge and epsilon parameters to zero, and setting the alpha value to 1.0 in the end state, and the kappa values to 1.0 in both end states.
All of the internals (bonds, angles, torsions) are kept the same at both end states.
>>> print(p.changed_bonds())
Empty DataFrame
Columns: [bond, length0, length1, k0, k1]
Index: []
>>> print(p.changed_angles())
Empty DataFrame
Columns: [angle, size0, size1, k0, k1
Index: []
>>> print(p.changed_torsions())
Empty DataFrame
Columns: [torsion, k0, k1, periodicity0, periodicity1, phase0, phase1]
Index: []
To decouple the benzene molecule correctly, a custom sire.cas.LambdaSchedule
is needed. This schedule turns off intermolecular interactions involving the
benzene, while keeping the intramolecular interactions the same.
The sire.morph.decouple() function creates a suitable schedule by
default, and attaches it to the merged molecule via its schedule
property.
>>> schedule = benzene.property("schedule")
>>> print(schedule)
LambdaSchedule(
decouple: (-λ + 1) * initial + λ * final
ghost-14::*: initial
ghost-14::kappa: -λ + 1
ghost/ghost::*: initial
ghost/ghost::kappa: -λ + 1
)
This schedule has a single stage called decouple. The default is that
all levers use the standard morphing equation to linearly interpolate
from the initial to final states. This has the effect of turning off
all charge and LJ interactions involving benzene.
However, we want to preserve the intramolecular charge and LJ interactions of benzene. Since all atoms are ghost atoms, these are all evaluated in the ghost/ghost and ghost-14 forces. We therefore set all levers in the ghost/ghost and ghost-14 forces to use the parameters in the initial state (i.e. the full charges and epsilon LJ parameters for benzene).
But, because the ghost/ghost force includes a correction to subtract a double-counted electrostatic interaction from the NonbondedForce, we also need to have a lever that scales kappa with 1-λ. In this way, the kappa parameter will ensure that the correction is applied at λ=0, when the electrostatic interactions of benzene are evaluated in both the NonbondedForce and the ghost/ghost and ghost-14 forces, while it will scale kappa to 0 at λ=1, when the electrostatic interactions of benzene are only evaluated in the ghost/ghost and ghost-14 forces.
We can view exactly how a schedule will perturb the real parameters of
a merged molecule using the
get_lever_values()
function.
>>> df = p.get_lever_values(schedule=schedule)
>>> print(df)
clj-charge-1 clj-charge-7 clj-epsilon-1 clj-epsilon-7 clj-alpha-1 ghost/ghost-kappa-1
λ
0.00 -0.1300 0.1300 0.363503 0.065318 0.00 1.00
0.01 -0.1287 0.1287 0.359868 0.064665 0.01 0.99
0.02 -0.1274 0.1274 0.356233 0.064012 0.02 0.98
0.03 -0.1261 0.1261 0.352598 0.063358 0.03 0.97
0.04 -0.1248 0.1248 0.348963 0.062705 0.04 0.96
... ... ... ... ... ... ...
0.96 -0.0052 0.0052 0.014540 0.002613 0.96 0.04
0.97 -0.0039 0.0039 0.010905 0.001960 0.97 0.03
0.98 -0.0026 0.0026 0.007270 0.001306 0.98 0.02
0.99 -0.0013 0.0013 0.003635 0.000653 0.99 0.01
1.00 0.0000 0.0000 0.000000 0.000000 1.00 0.00
[101 rows x 6 columns]
>>> ax = df.plot()
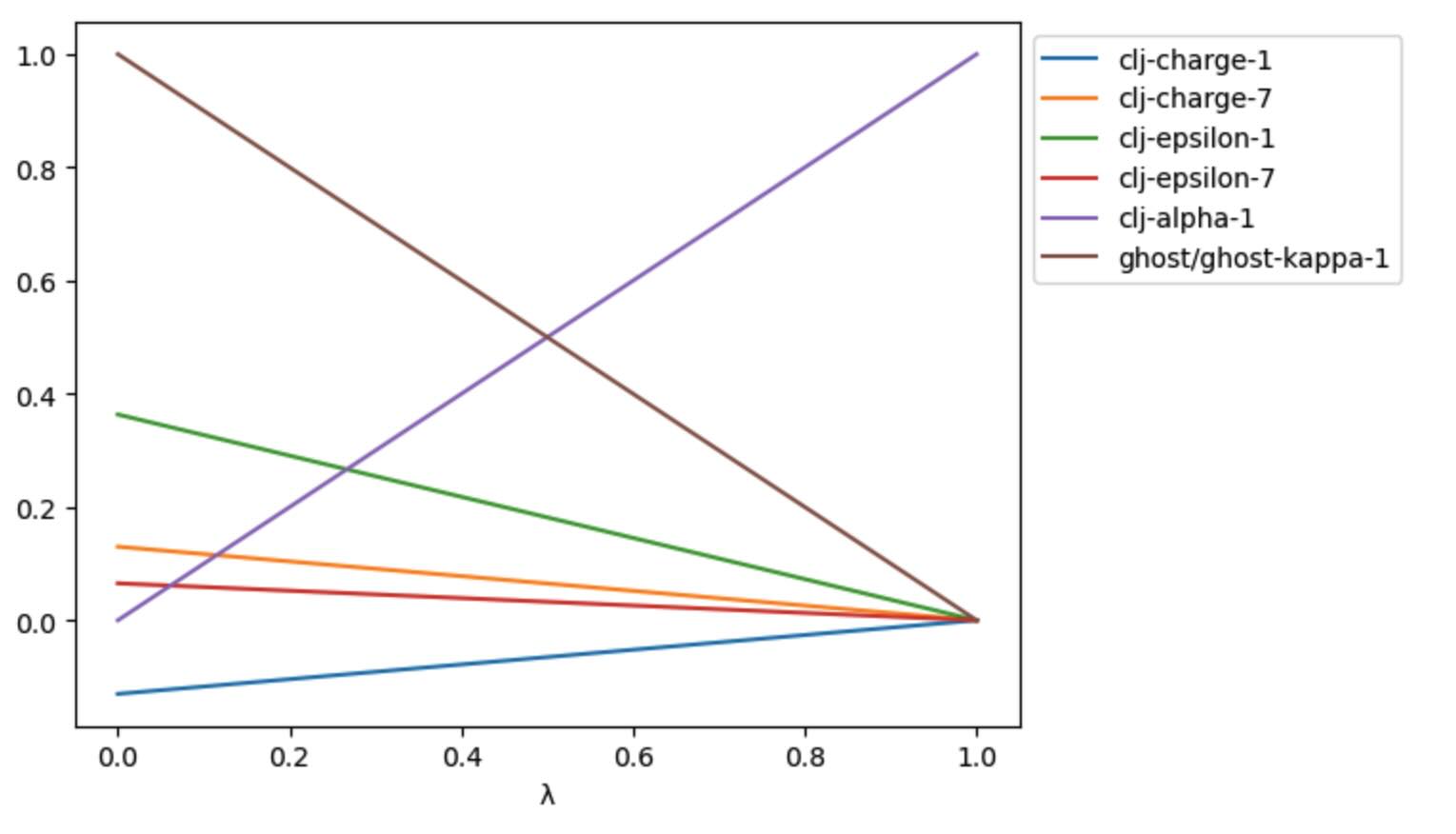
Running a decoupling simulation¶
We can run a decoupling simulation in the same way as any other free energy simulation.
First, we will update the system to use the decoupled benzene molecule.
>>> mols.update(benzene)
This works because we used as_new_molecule=False when creating
the merged molecule, so it kept its original molecule number.
Next, we will create a simulation object.
>>> d = mols.dynamics(timestep="2fs", temperature="25oC",
... schedule=schedule, lambda_value=1.0)
>>> d.run("100ps", lambda_windows=[0.0, 0.5, 1.0])
>>> print(d.energy_trajectory())
EnergyTrajectory( size=4
time lambda 0.0 0.5 1.0 kinetic potential
25 1.0 2.49529e+06 -8686.04 -8895.63 1583.95 -8895.63
50 1.0 1.54343e+06 -8750.01 -8914.34 1527.78 -8914.34
75 1.0 2.20708e+08 -8465.13 -8872.06 1624.18 -8872.06
100 1.0 1.02181e+11 -8534.06 -8949.38 1537.6 -8949.38
)
Note
We expect the energies at λ=0 to be high in this case, as the simulation was run at λ=1, where the benzene is not interacting with the the rest of the system, and thus free to overlap with other atoms.
Annihilation¶
Annihilation is the process of turning off all interactions involving all of the atoms of the molecule being annihilated. Note that this will also turn off all intramolecular interactions, so care must be taken to use restraints to prevent the simulation exploding.
You can create an annihilated molecule using the sire.morph.annihilate().
>>> benzene = sr.morph.annihilate(benzene, as_new_molecule=False)
>>> print(benzene)
Molecule( BEN:2 num_atoms=12 num_residues=1 )
Note
As before, we pass in as_new_molecule=False so that the resulting merged
molecule keeps the same molecule number as the original benzene.
The annihilated benzene molecule is a merged molecule where all of the atoms are converted to ghost atoms, and all of the intramolecular interactions are turned off.
>>> p = benzene.perturbation().to_openmm()
>>> print(p.changed_atoms())
atom charge0 charge1 sigma0 sigma1 epsilon0 epsilon1 alpha0 alpha1 kappa0 kappa1
0 C:1 -0.13 0.0 0.348065 0.348065 0.363503 0.0 0.0 1.0 1.0 1.0
1 C2:2 -0.13 0.0 0.348065 0.348065 0.363503 0.0 0.0 1.0 1.0 1.0
2 C3:3 -0.13 0.0 0.348065 0.348065 0.363503 0.0 0.0 1.0 1.0 1.0
3 C4:4 -0.13 0.0 0.348065 0.348065 0.363503 0.0 0.0 1.0 1.0 1.0
4 C5:5 -0.13 0.0 0.348065 0.348065 0.363503 0.0 0.0 1.0 1.0 1.0
5 C6:6 -0.13 0.0 0.348065 0.348065 0.363503 0.0 0.0 1.0 1.0 1.0
6 H1:7 0.13 0.0 0.257258 0.257258 0.065318 0.0 0.0 1.0 1.0 1.0
7 H2:8 0.13 0.0 0.257258 0.257258 0.065318 0.0 0.0 1.0 1.0 1.0
8 H3:9 0.13 0.0 0.257258 0.257258 0.065318 0.0 0.0 1.0 1.0 1.0
9 H4:10 0.13 0.0 0.257258 0.257258 0.065318 0.0 0.0 1.0 1.0 1.0
10 H5:11 0.13 0.0 0.257258 0.257258 0.065318 0.0 0.0 1.0 1.0 1.0
11 H6:12 0.13 0.0 0.257258 0.257258 0.065318 0.0 0.0 1.0 1.0 1.0
>>> print(p.changed_bonds())
bond length0 length1 k0 k1
0 C2:2-C3:3 0.138719 0.138719 301905.092179 0.0
1 C:1-C2:2 0.138719 0.138719 301905.092179 0.0
2 C6:6-H6:12 0.108536 0.108536 332422.631707 0.0
3 C5:5-H5:11 0.108536 0.108536 332422.631707 0.0
4 C4:4-H4:10 0.108536 0.108536 332422.631707 0.0
5 C3:3-H3:9 0.108536 0.108536 332422.631707 0.0
6 C5:5-C6:6 0.138719 0.138719 301905.092179 0.0
7 C2:2-H2:8 0.108536 0.108536 332422.631707 0.0
8 C4:4-C5:5 0.138719 0.138719 301905.092179 0.0
9 C:1-H1:7 0.108536 0.108536 332422.631707 0.0
10 C:1-C6:6 0.138719 0.138719 301905.092179 0.0
11 C3:3-C4:4 0.138719 0.138719 301905.092179 0.0
To annihilate the benzene molecule correctly, a custom sire.cas.LambdaSchedule
is needed.
The sire.morph.annihilate() function creates a suitable schedule by
default, and attaches it to the merged molecule via its schedule
property.
>>> schedule = benzene.property("schedule")
>>> print(schedule)
LambdaSchedule(
annihilate: initial * (-λ + 1) + final * λ
)
As before, we can view exactly how a schedule will perturb the real parameters
of a merged molecule using the
get_lever_values()
function.
>>> df = p.get_lever_values(schedule=schedule)
>>> print(df)
clj-charge-1 clj-charge-7 clj-epsilon-1 ... angle-angle_k-5 torsion-torsion_k-1 torsion-torsion_k-3
λ ...
0.00 -0.1300 0.1300 0.363503 ... 484.492886 1.534133 15.321516
0.01 -0.1287 0.1287 0.359868 ... 479.647957 1.518792 15.168300
0.02 -0.1274 0.1274 0.356233 ... 474.803028 1.503451 15.015085
0.03 -0.1261 0.1261 0.352598 ... 469.958099 1.488109 14.861870
0.04 -0.1248 0.1248 0.348963 ... 465.113170 1.472768 14.708655
... ... ... ... ... ... ... ...
0.96 -0.0052 0.0052 0.014540 ... 19.379715 0.061365 0.612861
0.97 -0.0039 0.0039 0.010905 ... 14.534787 0.046024 0.459645
0.98 -0.0026 0.0026 0.007270 ... 9.689858 0.030683 0.306430
0.99 -0.0013 0.0013 0.003635 ... 4.844929 0.015341 0.153215
1.00 0.0000 0.0000 0.000000 ... 0.000000 0.000000 0.000000
[101 rows x 14 columns]
The key difference between the annihilation schedule and the decoupling schedule is that the annihilation schedule linearly scales down all interactions involving the atoms of the molecule being annihilated, rather than only turning off the intermolecular interactions.
Running an annihilation simulation¶
We can run an annihilation simulation in the same way as any other free energy simulation.
First, we will update the system to use the annihilated benzene molecule.
>>> mols.update(benzene)
This works because we used as_new_molecule=False when creating
the merged molecule, so it kept its original molecule number.
Next, we will create a simulation object.
>>> d = mols.dynamics(timestep="2fs", temperature="25oC",
... schedule=schedule, lambda_value=1.0)
>>> d.run("100ps", lambda_windows=[0.0, 0.5, 1.0])
>>> print(d.energy_trajectory())
EnergyTrajectory( size=4
time lambda 0.0 0.5 1.0 kinetic potential
25 1.0 2.20919e+08 3.70208e+06 -8898.02 1561.3 -8898.02
50 1.0 2.73685e+07 1.26643e+07 -8863.57 1591.31 -8863.57
75 1.0 2.49653e+07 1.24605e+07 -8894.69 1611.1 -8894.69
100 1.0 1.20317e+09 1.90568e+07 -8908.07 1516.37 -8908.07
)
Note
We expect the energies at all values except λ=1 to be very high in this case, as the simulation was run at λ=1, where the atoms of the benzene are not interacting with the the rest of the system, and thus free to overlap with other atoms, and also be too far from each other to give sensible energies for their intramolecular interactions.
Ideally, in the above simulation you should add positional restraints to all atoms in benzene which gradually switch on to hold the atoms in position as their interactions are annihilated. The end state would represent non-interacting particles in harmonic wells, for which an analytical solution exists to calculate the free energy of annihilation.
While this is not covered in this tutorial, future versions of
sire will include tools to help with this.