Measuring Energies Across Trajectories¶
Just as you can make measurements across frames of a trajectory, you can also calculate energies across frames of a trajectory.
For example, let’s now load a trajectory for the aladip system…
>>> mols = sr.load(sr.expand(sr.tutorial_url, ["ala.top", "ala.traj"]))
If you are in a Jupyter notebook or similar you can view the trajectory using
>>> mols.view()
You can play the trajectory by clicking the play button.
There are multiple ways that you can calculate the energy of each frame of the trajectory. You could do it yourself in a loop, e.g.
>>> for frame in mols.trajectory()[0:5]:
... print(frame.energy())
-5919.77 kcal mol-1
-5974.75 kcal mol-1
-5928.36 kcal mol-1
-5917.37 kcal mol-1
-5968.4 kcal mol-1
calculates the total energy of the molecules for the first five frames of the trajectory.
You could also calculate this by using the apply function, as you
did for measurements.
>>> print(mols.trajectory()[0:5].apply("energy"))
[-5919.77 kcal mol-1, -5974.75 kcal mol-1, -5928.36 kcal mol-1, -5917.37 kcal mol-1, -5968.4 kcal mol-1]
You can use the name of the function, or can supply you own custom function, e.g.
>>> print(mols.trajectory()[0:5].apply(
... lambda frame: frame[0].energy(frame["water"])) )
[-52.8993 kcal mol-1, -46.7754 kcal mol-1, -45.9996 kcal mol-1, -53.2822 kcal mol-1, -57.4076 kcal mol-1]
calculates the energy between the first molecule and the water molecules for the first five frames.
The simplest way though is to the use the energy()
function of Trajectory.
>>> print(mols.trajectory().energy())
frame time 1-4_LJ 1-4_coulomb LJ ... dihedral improper intra_LJ intra_coulomb total
0 0 0.200000 3.509838 44.810452 912.765545 ... 9.800343 0.485545 -1.311255 -45.398213 -5919.765132
1 1 0.400000 2.700506 47.698455 919.494743 ... 11.776295 1.131481 -1.617496 -48.137252 -5974.747050
2 2 0.600000 2.801076 43.486411 829.127388 ... 11.614774 0.124729 -1.103966 -44.458051 -5928.356098
3 3 0.800000 3.365638 47.483966 949.652061 ... 11.383852 0.339333 -0.983872 -48.191512 -5917.368579
4 4 1.000000 3.534830 48.596027 906.780763 ... 10.214994 0.255331 -1.699613 -48.393889 -5968.402629
.. ... ... ... ... ... ... ... ... ... ... ...
495 495 99.199997 2.665994 42.866319 890.741916 ... 9.875872 0.356887 -1.584092 -44.220005 -5778.616773
496 496 99.400002 3.062467 44.852774 907.572910 ... 10.548897 0.327064 -1.814718 -44.419100 -5707.182338
497 497 99.599998 3.530233 44.908117 886.446977 ... 10.223964 1.006034 -0.692972 -44.902056 -5737.309043
498 498 99.800003 3.511116 42.976288 842.364851 ... 10.841436 0.518190 -1.862433 -43.205034 -5743.862524
499 499 100.000000 3.768998 41.625135 816.979680 ... 11.889372 0.846805 -1.897328 -44.306437 -5716.669273
[500 rows x 13 columns]
This performs the calculation for each frame, returning the result as a pandas
dataframe. If you are in a Jupyter notebook or similar, you can create
a graph of this using the pretty_plot function (or the standard pandas
plotting functions), e.g. plotting the energy for every frame gives
>>> mols.trajectory().energy().pretty_plot()
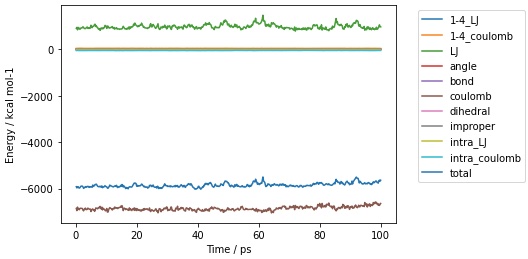
Calculating energies of selections¶
Just as for single-point energies, you can also calculate energies of selections across a trajectory.
For example, here is the energy for the first molecule for every frame;
>>> print(mols[0].trajectory().energy())
frame time 1-4_LJ 1-4_coulomb angle bond dihedral improper intra_LJ intra_coulomb total
0 0 0.200000 3.509838 44.810452 7.570059 4.224970 9.800343 0.485545 -1.311255 -45.398213 23.691739
1 1 0.400000 2.700506 47.698455 12.470519 2.785874 11.776295 1.131481 -1.617496 -48.137251 28.808384
2 2 0.600000 2.801076 43.486411 11.607753 2.023439 11.614774 0.124729 -1.103966 -44.458050 26.096167
3 3 0.800000 3.365638 47.483966 6.524609 0.663454 11.383852 0.339333 -0.983872 -48.191511 20.585470
4 4 1.000000 3.534830 48.596027 6.517530 2.190370 10.214994 0.255331 -1.699613 -48.393885 21.215584
.. ... ... ... ... ... ... ... ... ... ... ...
495 495 99.199997 2.665994 42.866319 11.339087 4.172684 9.875872 0.356887 -1.584092 -44.220004 25.472748
496 496 99.400002 3.062467 44.852774 9.268408 1.878366 10.548897 0.327064 -1.814718 -44.419098 23.704160
497 497 99.599998 3.530233 44.908117 10.487378 4.454670 10.223964 1.006034 -0.692972 -44.902059 29.015366
498 498 99.800003 3.511116 42.976288 9.017446 0.809064 10.841436 0.518190 -1.862433 -43.205031 22.606076
499 499 100.000000 3.768998 41.625135 13.629923 1.089916 11.889372 0.846805 -1.897328 -44.306436 26.646386
[500 rows x 11 columns]
while here is the interaction energy between the first molecule and all of the water molecules
>>> print(mols[0].trajectory().energy(mols["water"]))
frame time LJ coulomb total
0 0 0.200000 -16.737847 -36.161409 -52.899257
1 1 0.400000 -9.301014 -37.474372 -46.775387
2 2 0.600000 -18.171437 -27.828126 -45.999562
3 3 0.800000 -17.793606 -35.488562 -53.282168
4 4 1.000000 -12.819129 -44.588454 -57.407583
.. ... ... ... ... ...
495 495 99.199997 -11.093081 -36.438605 -47.531686
496 496 99.400002 -14.898056 -29.568473 -44.466528
497 497 99.599998 -10.513597 -35.824760 -46.338358
498 498 99.800003 -12.565213 -35.923033 -48.488247
499 499 100.000000 -7.696405 -41.844028 -49.540432
[500 rows x 5 columns]
and here is the energy between the carbon atoms in the first molecule and all of the non-carbon atoms in the first molecule
>>> print(mols[0]["element C"].trajectory().energy(mols[0]["not element C"]))
frame time 1-4_LJ 1-4_coulomb angle bond dihedral improper intra_LJ intra_coulomb total
0 0 0.200000 1.424470 54.597537 7.512649 4.194598 9.800343 0.485545 -0.844606 -15.571905 61.598631
1 1 0.400000 0.791583 52.969358 12.008645 1.821351 11.776295 1.131481 -0.937170 -17.901480 61.660062
2 2 0.600000 1.533581 53.594240 11.531951 1.623215 11.614774 0.124729 -0.885362 -16.394078 62.743051
3 3 0.800000 1.644253 53.721723 6.478095 0.614500 11.383852 0.339333 -0.950609 -19.388795 53.842352
4 4 1.000000 1.609999 53.472406 6.515561 1.965713 10.214994 0.255331 -1.010526 -21.909819 51.113659
.. ... ... ... ... ... ... ... ... ... ... ...
495 495 99.199997 1.324959 51.009025 11.173632 3.007010 9.875872 0.356887 -0.907750 -17.684035 58.155600
496 496 99.400002 1.310871 51.685638 8.855937 1.300661 10.548897 0.327064 -0.896125 -22.184101 50.948842
497 497 99.599998 2.073824 51.499993 10.461966 2.345364 10.223964 1.006034 -0.867677 -20.452924 56.290544
498 498 99.800003 1.357558 50.525535 8.838606 0.306832 10.841436 0.518190 -0.940949 -18.327720 53.119488
499 499 100.000000 1.783374 50.771940 13.388107 0.649792 11.889372 0.846805 -0.883830 -19.271354 59.174206
[500 rows x 11 columns]
Calculating energies for each view in a selection¶
Similarly, you can use the energies() function
to calculate the energies of each view in a selection. For example,
to calculate the energy between each residue in the first molecule and all
the water molecules use
>>> print(mols[0].residues().trajectory().energies(mols["water"]))
frame time LJ(ACE:1) LJ(ALA:2) LJ(NME:3) ... coulomb(ALA:2) coulomb(NME:3) total(ACE:1) total(ALA:2) total(NME:3)
0 0 0.200000 -6.223427 -5.550336 -4.964084 ... -21.074595 -5.258177 -16.052065 -26.624932 -10.222260
1 1 0.400000 -3.242855 -3.941213 -2.116947 ... -20.348710 -7.942912 -12.425605 -24.289923 -10.059858
2 2 0.600000 -5.742510 -6.968491 -5.460435 ... -15.125554 -3.010830 -15.434253 -22.094045 -8.471265
3 3 0.800000 -5.575444 -6.994749 -5.223413 ... -19.412484 -4.398933 -17.252589 -26.407233 -9.622346
4 4 1.000000 -4.911613 -3.534494 -4.373022 ... -23.911765 -6.041907 -19.546395 -27.446259 -10.414929
.. ... ... ... ... ... ... ... ... ... ... ...
495 495 99.199997 -2.225835 -7.586764 -1.280482 ... -11.946776 -6.009359 -20.708305 -19.533540 -7.289841
496 496 99.400002 -4.870466 -5.693474 -4.334115 ... -13.086695 -2.485933 -18.866311 -18.780169 -6.820047
497 497 99.599998 -2.317239 -5.137583 -3.058775 ... -15.248816 -4.309371 -18.583812 -20.386399 -7.368146
498 498 99.800003 -2.874906 -6.254290 -3.436018 ... -17.124897 -3.969899 -17.703143 -23.379187 -7.405917
499 499 100.000000 -4.570392 -2.671509 -0.454505 ... -17.341576 -5.990427 -23.082416 -20.013085 -6.444933
[500 rows x 11 columns]
or to calculate the energy between each individual carbon atom in the first molecule, and all non-carbon atoms, use
>>> print(mols[0].atoms("element C").trajectory().energies(mols[0]["not element C"]))
frame time 1-4_LJ(C:15) 1-4_LJ(C:5) ... total(CA:9) total(CB:11) total(CH3:19) total(CH3:2)
0 0 0.200000 0.172479 0.145310 ... 0.734309 10.422320 12.830321 -7.916957
1 1 0.400000 0.068533 0.293878 ... 0.833780 10.329925 12.680069 -5.459349
2 2 0.600000 0.277433 0.119361 ... 2.105670 9.903695 12.342441 -8.597333
3 3 0.800000 0.218850 0.293046 ... 0.648526 8.335720 11.774262 -5.820661
4 4 1.000000 0.272544 0.131482 ... 1.613490 8.462497 11.444502 -5.993019
.. ... ... ... ... ... ... ... ... ...
495 495 99.199997 0.084804 0.092928 ... 2.501087 8.260509 13.692395 -8.903780
496 496 99.400002 0.301822 0.055070 ... 0.860013 7.782723 12.373809 -9.595075
497 497 99.599998 0.287670 0.167273 ... 0.810351 8.201226 12.855330 -10.161720
498 498 99.800003 0.247033 0.071368 ... 0.636738 8.162127 12.441049 -11.020026
499 499 100.000000 0.762106 0.001875 ... 0.772173 8.378594 12.675099 -9.996188
[500 rows x 46 columns]
or you can calculate the energy between the first two residues of the first molecule, and the last residue of that molecule,
>>> print(mols[0].residues()[0:2].trajectory().energies(mols[0].residues()[-1]))
frame time 1-4_LJ(ALA:2) ... intra_coulomb(ALA:2) total(ACE:1) total(ALA:2)
0 0 0.200000 0.804882 ... -21.180433 -0.623493 11.417398
1 1 0.400000 0.345863 ... -19.744563 -0.887233 11.519219
2 2 0.600000 0.570195 ... -20.630107 -0.486087 10.305274
3 3 0.800000 0.583037 ... -20.152031 -0.744566 11.144469
4 4 1.000000 0.865922 ... -20.661027 -0.736126 11.418229
.. ... ... ... ... ... ... ...
495 495 99.199997 1.541341 ... -25.465191 0.631658 8.578779
496 496 99.400002 0.881839 ... -24.581280 0.339605 10.761385
497 497 99.599998 1.974929 ... -25.758041 0.272158 12.628546
498 498 99.800003 1.860815 ... -25.768444 0.550181 9.597360
499 499 100.000000 1.335519 ... -25.910358 0.396877 8.686331
[500 rows x 17 columns]
As before, all of the above are returned as pandas dataframes, and so can be
plotted using the standard pandas functions, or via the pretty_plot function
that is added by sire when the energies are calculated, e.g.
>>> mols[0].residues()[0:2].trajectory().energies(mols[0].residues()[-1]).pretty_plot()
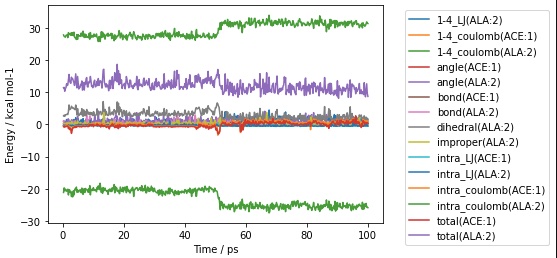
Note how the column names for these dataframes include both the energy component
and an identifier for the view. You can programmatically generate these
column names using the sire.colname() function e.g.
>>> print(sr.colname(mols[0].residues()[0], "total"))
total(ACE:1)
gives the column name for the total energy component for the first residue.
Calculating energies where the selection changes per frame¶
The energy() and energies()
functions calculate energies using static selections for each frame. This
means that the selection is made before calculating the energy, and then
this selection is used for each energy calculation.
This is a problem if the selection is based on something that would change in each frame, e.g. for example the coordinates of the atoms. For example, here we try to calculate the energy between the first molecule and all water molecules that are within 5 Å.
>>> print(mols[0].trajectory().energy(mols["water and molecule within 5 of molidx 0"]))
frame time LJ coulomb total
0 0 0.200000 -13.634133 -33.715126 -47.349259
1 1 0.400000 -6.036615 -36.208598 -42.245213
2 2 0.600000 -14.882135 -27.783208 -42.665343
3 3 0.800000 -14.223444 -34.152490 -48.375934
4 4 1.000000 -9.143589 -43.110359 -52.253948
.. ... ... ... ... ...
495 495 99.199997 0.293104 -3.264990 -2.971886
496 496 99.400002 -1.536769 -0.334118 -1.870887
497 497 99.599998 -0.742696 -3.797462 -4.540158
498 498 99.800003 -0.568741 -5.099334 -5.668075
499 499 100.000000 -1.961059 -1.866724 -3.827783
[500 rows x 5 columns]
This clearly hasn’t done what we want, because the energy trends towards zero over time. This is because the selection of water molecules is fixed, and was not updated for every frame. The selected water molecules diffused away, and so the energy trended towards zero.
You need to manually update the selection if you want it to update for every frame. You could do this via a loop, e.g.
>>> for frame in mols.trajectory():
... print(frame[0].energy(frame["water and molecule within 5 of molidx 0"]))
-47.3493 kcal mol-1
-43.1736 kcal mol-1
-44.3147 kcal mol-1
-49.283 kcal mol-1
-53.6223 kcal mol-1
...
-40.8416 kcal mol-1
-38.6555 kcal mol-1
-38.1635 kcal mol-1
-42.4407 kcal mol-1
-42.367 kcal mol-1
or by using apply
>>> print(mols.trajectory().apply(
... lambda frame: frame[0].energy(frame["water and molecule within 5 of molidx 0"])) )
[-47.3493 kcal mol-1, -43.1736 kcal mol-1, -44.3147 kcal mol-1,
-49.283 kcal mol-1, -53.6223 kcal mol-1, -54.09 kcal mol-1,
...
-42.5333 kcal mol-1, -40.8416 kcal mol-1, -38.6555 kcal mol-1,
-38.1635 kcal mol-1, -42.4407 kcal mol-1, -42.367 kcal mol-1]